小学校プログラミング教育のねらいとは何か。どう実践するか。
小学校プログラミング教育のねらいは3点
文部科学省の「小学校プログラミング教育の手引き」で示されているねらいを要約すると以下の3点になります。
- ①プログラミング的思考を育む
- ②プログラムの働きや良さ、重要性に気付き、コンピューターをうまく活用して身近な問題等を解決する態度を育む
- ③各教科での学びをより確実なものとする
これらについて具体的には何をしていけばいいのかを、今回から数回に分けてお話ししていきたいと思います。なお、この記事は主に小学校の先生、小学生のお子さんを持つ両親、保護者の方々に向けた内容となりますが、プログラマーを目指す方、プログラマーとしての自信がない方にも読んでいただきたい内容です。
プログラミング的思考を育むには、それを意識した行動を繰り返す。
私の過去の記事(プログラミング教育が小学校で必修化されるけど大丈夫?)でも書きましたが、プログラミング的思考はプログラミングを通じて育まれるのではなく、普段からそれに則した行動をすることで育まれると思います。
小学生がプログラミングそのものを学習する必要はなく、また学校で教えることにも無理があると思います。一方で、本来のねらいであるプログラミング的思考を育むことは、簡単ではありませんが、大人になった時や他の教科の勉強にも役立つと思います。
まず、プログラミング的思考がどういうものかが良くわからないと思いますので、私なりに説明したいと思います。全体をイメージすると下の図のようになります。
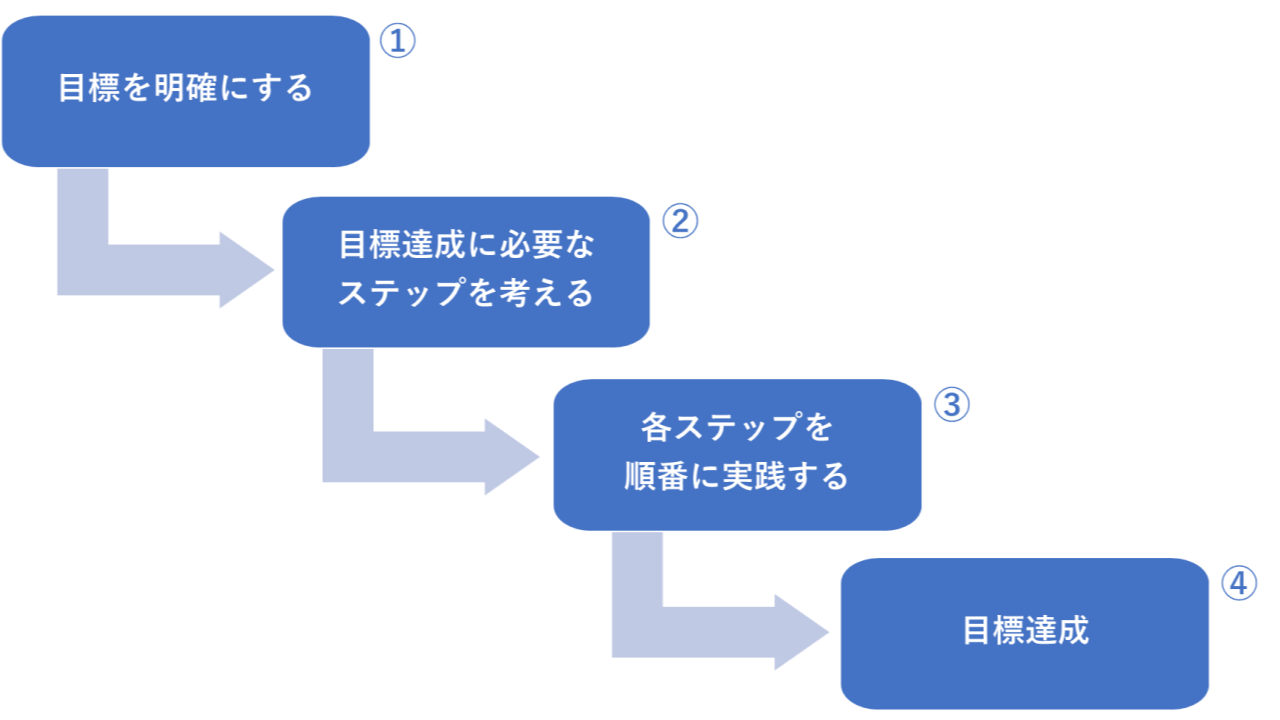
プログラミング的思考の全体イメージです。①から④までを順に行いますが、途中で問題があれば前に戻って見直しながら進めます。
ここから、これら①~④について詳しく説明していきますが、一旦、プログラミングのことは忘れて考えてみてください。
① 目標を明確にする
まずは目標・ゴール、言い換えれば「何をしたいのか」を明確にすることから始まります。文部科学省からプログラミング学習の事例として出されている「正多角形をかく」を例に考えてみます。
「人とは相談しないで正多角形を1つかいて」と30人の生徒に言ったとします。ここで、正多角形とは何かは全員が理解しているものとします。
ここで、30人がかいた答えはどうなるか想像してみてください。
すると、正三角形や正方形、正六角形など様々な図形ができあがるはずです。また正三角形をかいた生徒の中でも、大きさや傾きがそれぞれ違っているはずですよね。これはどれも正解ですが、先生が求めていた答えとは違うかもしれません。これは最初に与えた目標があいまいだからおきます。あいまいさをできるだけ排除して目標を明確にしなければ、達成したときの成果は大きく異なってしまします。
全員が同じ図形をかくことを求めているのであれば、「1辺の長さが3cmの正三角形をかいて」と言えば全員が同じ大きさの正三角形を書けます。さらに「頂点の内の1つが左右の中心」、または「底辺が水平」という条件を付け加えれば傾きも一緒になるはずです。
ここでは、皆が同じ図形をかくことが正解だと言いたいわけではありません。目標はできるだけ明確な方がやるべきことも明解になり、考えやすいということです。
② 目標達成に必要なステップを考える
次に「1辺の長さが3cmの正三角形をかく」という目標を達成するためのステップ、言い換えれば「何をどのような順番で行えばよいか」を考えていきます。ここでは図形の傾きは考えないことにしましょう。
例えば以下の様に考えたとします。
Step.1 3cmの直線を1本引く
Step.2 最初に引いた直線の片方の端から60°の傾きで3cmの直線を引く
Step.3 2本の直線の端を結ぶ直線を引く
人によっては、Step.1の前後どちらかに内角(60°)を求めるステップが入るかもしれません。今回そこは暗黙のうちにわかっているためステップとして現れていませんが、どちらでも問題ありません。
ところが、このステップを自分で実践する上では何の問題もないのですが、「正三角形をかく」という目標を伝えずに他人に同じステップを実践してもらうと、結果は正三角形にならないことがあります。
理由は
Step.2の「60°の傾き」にあいまいさが含まれているから
です。下の図を見てください。
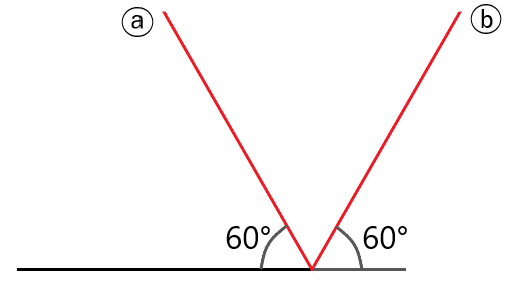
60°の傾きの直線を表した図です。一番下の黒線が1番目のStep.1でかいた直線、赤線が「60°の傾き」の直線です。
正三角形をかくという目標がわかっていれば何の疑問もなくⓐの赤線をイメージするでしょう。これは、「2つの直線の交わる角が60°」という暗黙のルールがあることを知っているからです。
しかし、目標がわかっていなければ、暗黙のルールも知る由もなく、ⓑの赤線をイメージしてしまうかもしれません。
このように、あいまいさや暗黙的なことを排除できていないと、得られる結果が想定と異なったり、いつも同じ結果にならない原因になったりしてしまいます。
ですので、ここで考えるステップはより具体的に、あいまいさを徹底的に排除することが重要です。
(ちなみに、「2つの直線の交わる角が60°」となる直線はⓐ以外にもありますので考えてみてください。そちらでも最終的に正三角形が正しくかけるはずです。)
また、今回の正三角形の例では簡単なのですぐに順番にステップが考えられますが、難しい目標の場合は、最初は大まかなステップを考えて、それを1つずつ詳細にして考えます。
ちょっと難しいかもしれませんが、抽象化と具体化を繰り返して、最終的に曖昧さを排除したステップを考えていくことが重要です。
抽象化と具体化を繰り返し、あいまいさ・暗黙のルールを排除して考えることが重要
ここまでで、目標と必要なステップを考えました。重要なことをまとめると以下の通りです。
目標はできるだけ明確にする
目標達成のステップは徹底してあいまいさ・暗黙のルールを排除する
考えるのが難しい場合は抽象化と具体化を繰り返して1つずつ考える
長くなってしまいましたので、続きは次回お話ししたいと思います。










この記事へのコメントはありません。